Generalization Error for Model Validation
Chris Fariss and I wrote an article (conditionally accepted at Political Science Research & Methods) which argues that the predictive validity of observational and quasi-experimental designs is maximized by minimizing generalization error. We think estimating generalization error is similar to external validity (which can be assessed by replication) but applicable in scenarios where replication (taking another draw from the data generating process) isn't possible: like with quasi-experiments or observational studies wherein the data are passively collected.
Below is a summary of what we discuss. Much of this is a discussion of statistical learning theory in the context of the social sciences.
Model Selection
I use the phrase "model selection" to refer to the process of selecting the complexity of a statistical model. This can be done according to some automated process like boosting or by an analyst manually modifying and comparing a series of structural regresson models wherein the complexity within each is fixed (i.e., a regression with a fixed number of parameters). In either case estimating each model involves finding a set of parameters which minimize a loss function, which measures the difference between predictions and observations.
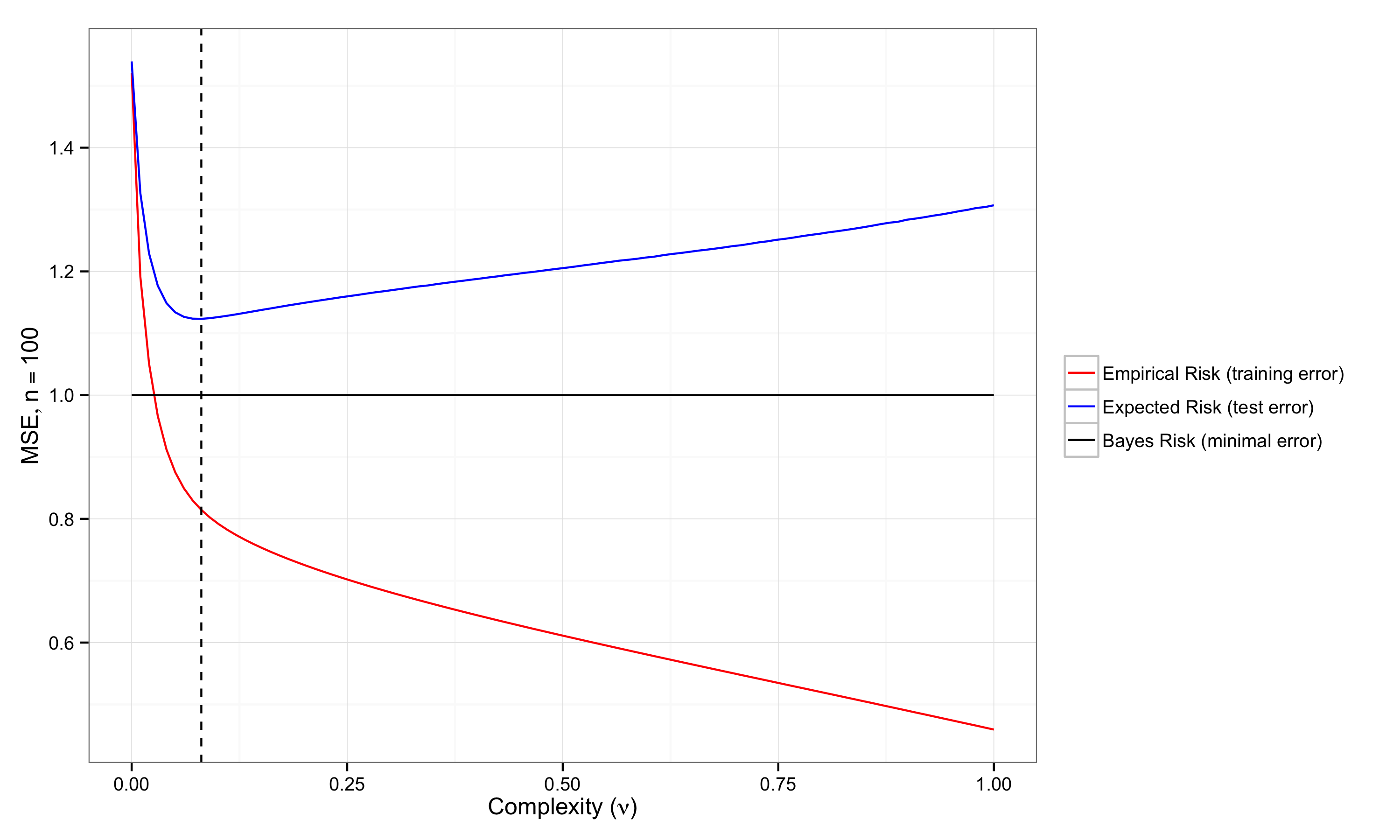
Minimizing the loss function over the training/sample data (empirical risk minimization) has the well known problem of optimism, which results from overfitting. An example of this is that $R^2$ always increases as covariates are added to a regression.
Less appreciated, at least explicitly, in the social science methodology literature, is the problem of underfitting: failing to discover generalizable structure in data. In-sample measures of predicitive validity are less biased when the data are underfit, but the sample re-use bias problem remains. Furthermore, due to the complexity of the social world and the extraordinary simplicity assumed by most statistical models estimated using observational or quasi-experimental data in the social sciences, there likely is generalizable information left undiscovered in much of our data.
Both overfitting and underfitting are best understood as extremes of the bias-variance tradeoff (i.e., if you've overfit you've traded too much variance for a reduction in bias, and vice versa for underfitting). Although bias and variance are usually discussed in the social science methodology literature in the context of estimating "effects" by regression, it applies equally to predictions. Bias is the difference between the average prediction and the observed outcome if data were drawn from the data distribution an infinite number of times and the regression estimated on each draw. Variance refers to how wide the distribution of predictions is. Clearly being right on average is useless if the variability of the predictions is so wide that for any particular prediction you are very far from correct: both bias and variance matter. There is a tradeoff that is not 1-1 between bias and variance, so it often makes sense to trade one for the other to minimize error.
Estimating/Bounding Generalization Error
This motivates the minimization of generalization error, which is the expected loss over the data distribution, i.e., the average loss over all the theoretically possible data. Since we don't have access to the data distribution (because data were passively collected, were expensive to collect, etc.), people have developed a variety of clever ways to avoid the optimism that comes from re-using the whole sample to estimate generalization error. Most of these methods are Monte-Carlo resampling methods which treat the sample data as the data distribution, and repeatedly psuedo-sample from it in a way that is supposed to mimic the sampling process that gave us the sample data. Since only a random psuedo-sample of the sample data is available, this reduces the problem of optimism.
However, when drawing psuedo-samples from the observed data results in psuedo-samples that are dependent on one another, because, for example, the resampling method used presumes that the data are independent when that is not the case, the problem of optimism resurfaces since the Monte-Carlo variance reduction from averaging over the psuedo-samples will be smaller than if the pseudo-samples were independent.
One of the most important problems for social science methodologists is developing ways of estimating predictive performance with the sorts of data we have, with a myriad of dependence structures. There is a literature on resampling methods with dependent data but it in general presumes optimistically simple structures. One possibility I've been thinking about lately is nonparametric segementation (e.g., clustering) to establish exchangeable blocks which can then be resampled. I expect this probably works decently well, but I haven't actually verified that this is the case generally. Variations on this could estimate sampling weights which would work similarly.
An alternative, structural risk minimization relies on bounding the generalization error based on features of the data and the class of the model estimated. This appears to be mathematically difficult, though there have been a series of papers on the topic applied to macroeconomic time-series by Shalizi and others.
Flexible Statistical Methods
As is suggested in the above discussion of bias/variance and over/under-fitting, data-adaptive methods, i.e., methods which add parameters as the amount of data input increases, have generally lower bias and higher variance. Estimating the appropriate of bias to introduce allows variance to be reduced, sometimes substantially. This allows the use of methods capable of learning complex functions but which can also approximate simple functions when they are what underly the data. The key difficulty with increasing model complexity is interpretability. But I'm working on that.
In the mean time using semiparametric methods like model-based additive boosting or generalized additive models is attractive. Especially when there is such great software to do it (e.g., mgcv and mboost).