Zach Jones

An Empirical Evaluation of Explanations for State Repression

The code, data, manuscript, and appendix.

If you have any questions about the article, this post, the code, or anything else feel free to email me!

Daniel W. Hill Jr. and I recently wrote a paper forthcoming (now published) at the American Political Science Review which examines the ability of variables identified as important by the state repression literature to improve our ability to predict state repression. We don't think that null hypothesis significance testing (NHST) is an adequate way to assess the importance of a variable, since it does not prevent overfitting and is an imperfect measure of substantive significance. Neither of these points are new but they are not widely appreciated. Predictive validity suffers as a result of the exclusive use of NHST.

While our paper is directed primarily at the state repression literature, our points are applicable to many areas of political science. We evaluate the predictive power of a variety of variables using different measures of state repression with comparative cross-validation and random forests (see Strobl, Malley, and Tutz 2009 for an excellent introduction to the latter). Our main findings are that many of the variables identified in the literature as important do not improve our ability to predict state repression¹. The variables we find to be important across most/all of our dependent variables (country-year measures of state repression)² are:

• Polity IV (especially its participation competitiveness component)
• civil war (from UCDP/PRIO)
• judicial independence (from CIRI)
• oil rents (from Ross 2006 and used in DeMeritt and Young 2013)
• youth bulges (from Urdal 2006 and used in Nordas and Davenport 2013)

We think that the predictive power of both Polity and civil war are due to conceptual overlap with state repression though, so they aren't particularly interesting³. There is also a great deal of variation in the marginal predictive performance of the covariates across dependent variables, that is, some covariates do a better job predicting some types of repression than they do at others.

Judicial independence, constitutional guarantees for fair trials, and common law legal heritage, among others, all performed well (though not as well as the aforementioned variables), but seem to be somewhat under-studied relative to many of the variables that turned out to be poor predictors of state repression, some of which have been studied extensively. Generally we found that "international" variables were outperformed by "domestic" variables.

You can see a some of the results in the figures below. Both figures show the unscaled marginal permutation importance⁴ calculated from a fitted random forest for each dependent variable, as indicated by the grey bar at the top of each panel in the graph. The permutation importance shows the average reduction in out-of-bag⁵ classification performance (proportion of cases correctly classified) from permuting the values of the variable indicated by the y-axis. These scores are bootstrapped 100 times, and the .025 and .975 quantiles of the distribution of estimates are shown to get a sense of how stable the rankings are. We also compare the results across different tuning parameter choices in the appendix of the paper. Check out the paper for all of the details!

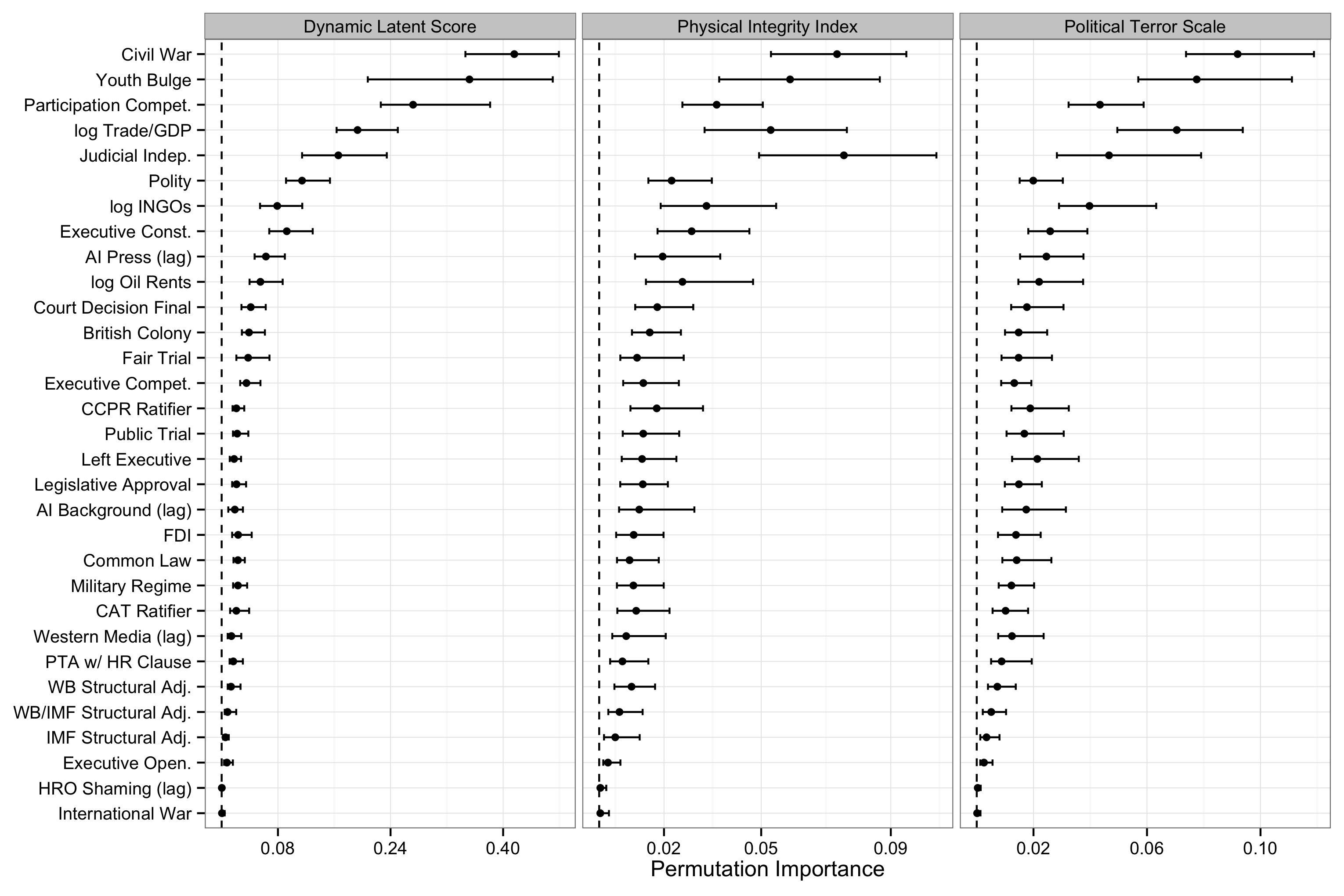
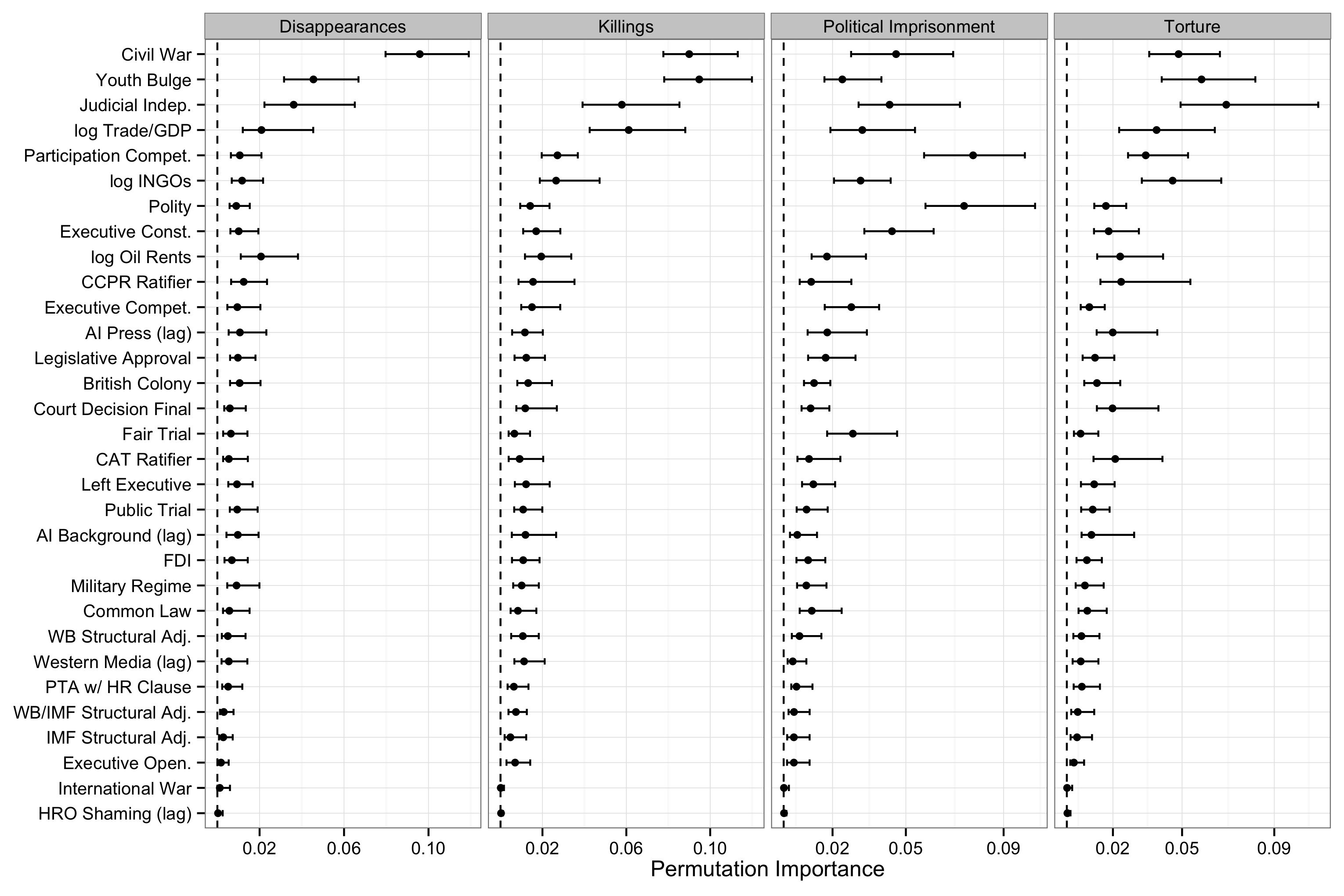
I find the results from the random forests to be the most interesting, since they make no assumptions about linearity and additivity, but the comparative cross-validation we conducted (which does make such assumptions) gives a rank ordering of variable importance (which is operationalized differently of course) that is similar to what we found with the random forests.

One of the points we make in the paper is that a number of variables we consider are more or less required to be in any model of state repression⁶. That this is the case suggests that there is a misunderstanding about the purpose of control variables in regression models where the goal is causal inference⁷. This is reinforced by the all-to-common refrain that the variable in question is an important predictor of repression, and thus must be included in the regression. If the goal is to do causal inference control variables are there to remove confounding: variables that are correlated with both state repression and the variable of interest. Thus, if the proposed control variable isn't a confounder then it is usually the case that it shouldn't be in your model. However, since social systems are so complex and our ability to collect the data we want is so limited, I am skeptical about our ability to identify the relevant set of confounders in observational data.

Some (maybe most) research in political science might be better classified as exploratory data anlaysis, in that it involves searching for reliable patterns in data rather than trying to recover an unbiased estimate of a single parameter. This is what I would classify our study as. Data mining (often synonymous with machine/statistical learning) is often a pejorative in political science, but is only problematic when it is done with methods that have poor properties for this task. Models with restrictive assumptions such as linearity and additivity are rarely justified theoretically or empirically; these are assumptions made out of convenience. I think that our default assumption should be that there is interaction and non-linearity in the data we are attempting to describe. This point has been made by some in political science (see Jackman and Beck 1998, Beck, King, and Zeng 2000, and Hainmuller and Hazlet 2013 for example) but it deserves a great deal more attention in my view.

The quantitative study of state repression is dominated by cross-country panel data sets. As has been pointed out numerous times now (see e.g., Freedman and Lane 1983, Berk, Western, and Weiss 1993, and Western and Jackman 1994) statistical inference doesn't make much since with these "apparent populations." Standard errors are estimates of the standard deviation of the sampling distribution of the test statistic in question and with an "apparent population" there is no sampling going on. $p$-values are derived from the sampling distribution of the test statistic under the assumption that the null hypothesis is true, and so they suffer from the same problem as the standard error, as do confidence intervals. However, if there is random assignment to treatment, or plausible as-if randomization, then inference can be appropriate.

Setting aside the "apparent population" problem, there are a number of other problems with the way $p$-values are generally used. Many of these proverbial drums have been beaten before (see Gill 1999, John Myles White's series on the topic: parts 1, 2, 3, 4, 5, and some of Andrew Gelman's commentary). $p$-values are not a measure of effect size. They measure the probability of observing a test statistic more extreme than the one you just calculated if you repeated the experiment/took another random sample, assuming that the null hypothesis is true. As I've already mentioned, this clearly doesn't make since outside of random assignment to treatment and/or random sampling from a population. The fact that $p$-hacking might be pervasive just makes the matter worse (see Gerber 2008, Ioannidis 2005, and Simmons 2011 for a discussion of $p$-hacking, Gelman is a bit nicer on this point).

In any case the question that hypothesis tests, $p$-values, and confidence intervals answer are not the questions that political scientists are generally asking. Most of the time it seems that political scientists want to know the size of the region that contains the "true" parameter value with probability .95 (the Bayesian interpretation), not that the confidence interval constructed will cover the true value 95% of the time⁸. This disconnect probably explains why confidence intervals are not generally given their frequentist interpretation. Lastly, it is rarely the case that any effect is truly zero. A null hypothesis of no effect is a bit silly, especially when the study has grossly exaggerated statistical power, as is the case where dependent data is assumed independent. This is a point that Andrew Gelman has talked about several times (see here and here).

These problems are pervasive but there is not any one solution to these problems. NHST is appropriate in some circumstances, but isn't in many of the situations in which it is used. Using Bayesian methods is not a panacea either, though I think they are more appropriate for many social science questions. The "solution" to these problems is a better connection between the method selected and the goal of the research. In many circumstances I think this means that we should be using more flexible, inductive methods, and using out-of-sample predictive error as a heuristic for deciding how much data reduction/smoothing to do.